[ home | contact dr. berk | archive ]

Science Archives:

Environmental Camping, Potato Clocks, and Whirlpool Disillusionment

Explosive Microwaved Water

Piercing and Beer

Bowling Balls and Pickle Electrocution Guidelines

Your Relative Worth

Space Age Polymers

The Dangers of Margarine, Spam, and Polystyrene

Some Cold, Hard Facts

Useful Measures

The Leap Second

Glowing Pickle

Potatoes

Wave Cannon

Margarine

Styrofoam

Bowling

Pick-up Lines

party poker

Please Pass the Science
by Dr. Scott Berk

Simplistic, misleading, and somewhat condescending. . . but never boring!

What is the origin of Earth's moon? When did the first multicellular organisms appear? Does George W. Bush qualify as a multicellular organism? Send in your burning science questions to "Please Pass the Science" in care of Dr. Berk.

05nov29. Doc asks the following question:

Dr. Berk:

Yes, this is kind of true. It is certainly harder to metabolize (which involves "recognition" and breaking down of molecules) saturated hydrocarbons, which are what you get when you hydrogenate fatty acids, than unsaturated ones. The hydrogenation process gets rid of a double bond, which is a key metabolic "hot-spot" that the body can recognize and "attack." Note that even though it's harder to get rid of unsaturated fat, it can still be dealt with by the body. That said, the body doesn't need that much fat, period, whether it is metabolizable or not. There are many naturally occurring saturated fats, so don't think of it as rendering something "natural" into something "artificial." Hydrogenation transforms unsaturated fats to saturated fats (which have better properties for use in food -- mainly that they are solid, rather than liquid, at room temperature -- think vegetable oil becoming margarine). Hope that helps.

2005nov28. Dr. Berk responds to criticisms of High-Fructose Corn Syrup.

Jane-

turned on
drool-y
hard packed
really long
fickle
suction

I never knew science could be so ... sensual!

Both corn starch/water and quicksand are non-Newtonian fluids and behave in the same way. Their viscosity increases with increasing applied force. What makes them so is not the size of the molecules, but the fact that they are concentrated colloidal suspensions with a relatively large particle size. The sand or starch particles are not really dissolved, but suspended, in the water. If the suspension is thick enough, you get a situation where all the particles are touching each other, but there's enough water around to allow them to slide past each other when you apply a slow force. If you stir too fast, however, the particles don't have time to get out of each other's way, and will "lock up," making the mixture seem solid. So, if you ever get stuck in quicksand, move slowly and deliberately. Thrashing about will just cause the quicksand to seize.

It really depends on you. Your professional bowling ball salesperson can help you decide what ball (or balls) is best for your particular throw and the varying lane conditions you may encounter. As I've said before, bowling is a beautiful and complex sport. I might also add that physics is pretty much involved in everything.

For an answer to at least part of your question, look here.

Acetone "dissolves" polystyrene because it, like polystyrene itself, is relatively non-polar. In other words, it is chemically more similar to polystyrene than more polar solvents like alcohol or water, for example. Other non-polar solvents, like hexane (a component of gasoline) or toluene (charcoal lighter fluid), will also do the trick.

As I understand it, one shouldn't microwave any plastic containers which contain plasticizers. These are chemical additives which are added to the material during manufacture to make it more "plastic" and less rigid. If present, the plasticizers can leach into your food even though the plastic does not deform. Even so, the small amount of plasticizer coming out of microwaved plastic is probably quite harmless. I'd be more concerned with the plastic melting and mixing with the food to form something that doesn't taste very good.

Now, I'm pretty sure that styrofoam doesn't contain plasticizers, so you're probably OK. It does melt at around the boiling point of water, so you should definitely make sure that you don't heat your food too much, or you'll end up with polystyrene soup! See this page for another response to this kind of question.

While it is possible to describe any continuous line as a mathematical function, I seriously doubt that such a function is routinely used to define a bowling pin. The best way to calculate volumes of irregularly shaped objects is to use the famous Archimedes method:

Put a container large enough to hold the object inside another container. Fill the inner container to the brim with water, then place the object in. The volume of water displaced into the outside container (which can be simply measured by weight or with measuring cups or the like) is the exact volume of the object.

Eckie- The most accepted theory is that Earth probably started with enough water. Chondrites are a type of planetesimal, the bodies which merged together to create the planets of the solar system (including Earth) some 4.6 billion years ago. They are about 0.1 percent water by weight, which ends up being more than enough to account for the total terrestrial volume of water. If for some reason this "built-in" water was lost to space during Earth's early days, it is hypothesized that enough other chondrites fell to Earth as meteors during the period up to about 3.8 billion years ago to fill the oceans.

An alternative theory is that the Earth has been constantly pelted by house-sized space snowballs (no, I am not making this up - after all, comets are just "dirty snowballs"), and the accumulated volume of these snowballs is enough to account for all the water on Earth. If this seems like a completely wacko theory, remember that until the big crater was found underneath Mexico in the early nineties, the whole "giant meteor impact" theory of dinosaur extinction was thought to be equally laughable by most of the scientific community. Some recent satellite imagery may have caught one of these "comet meteors" on the way down, so don't count the "space snowball theory" out!

For my response to a similar, but much more belligerent, question, go here.

Brandon- Some hardware stores sell zinc strips to prevent moss buildup on the roof. An alternative would be to use a galvanized (zinc coated) nail.

I think you've solved your own problem. When I bowl (and I'm quite the amateur, I can assure you), I find that the less I think about bowling, the better I do. Thus, increased alcohol consumption should lead to less concentrated thought, which in turn should lead to better overall bowling performance! Just be sure you sober up enough to drive home afterwards. I'm always happy to provide SCIENTIFIC justification for drinking.

A simple web search on "non-newtonian fluid" turned up this answer, which is delightfully succinct and contains other links:

http://www.madsci.org/posts/archives/mar97/856396884.Ph.r.html

To summarize, a Newtonian fluid has a constant viscosity at a constant temperature. The viscosity of a non-Newtonian fluid may change at any given temperature.

Brent- When you blow up a balloon, you are forcing air inside it. This increases the inside air pressure, causing the walls of the balloon the expand. A volume of gas exerts an equal force in all directions, so the shape of the balloon is dictated by the relative strength and flexibility of the rubber making up the balloon. Since the strength of the rubber in most balloons is relatively uniform, the shape of most balloons is spherical, representing an equal outward push of the air inside, and an equal response by the rubber in all directions. If you make a balloon where the rubber stretches more easily in one direction than another, you can get a cylindrical shape (often used to create balloon animals). The breaking point of the rubber is ultimately determined by the strength of the chemical bonds in the rubber. This, in turn is influenced by the thickness and the method used to produce the rubber. Polymer design is a very complex science, involving a lot of trial and error and observation. To date, there is no perfect model of polymers such that one could design, from scratch, a material that breaks at a particular pressure (although computational chemists are slowly getting better at this). The best way to do it is to try many different rigorously controlled conditions and remember which one caused the formation of the polymer with desirable properties.

Sorry to hear about the vanilla and almond failures - I have higher hopes for the honey. Definitely dissolve the honey in water. And I'd hazard that the warmer the solution, the better the chance that the flavor gets in - heat should open up the pores a bit - just don't pop the corn prematurely! See how easy it is to be a scientist?

Chris- In the summary of the second question's answer (see below), I said that if the rods were exactly parallel, they would intersect simultaneously. I didn't mention how you'd go about getting them to move toward each other while being parallel. Also, I was not assuming that the rods were very long. For the purposes of my answer, I was considering what would happen if two short rods (or a guillotine and a straight surface) were made to pass each other. With small enough rods, the initial point of force would propagate through the rod very quickly. It would not take very long before the rod came to a sort of equilibrium, with the velocity of all of the atoms in the rod reasonably in sync. Once you have this situation (one rod is moving at a constant velocity toward another one), it is possible to observe that the point of intersection (or the point where the rods appear to be passing each other) can move faster than light. Note that the rods themselves do not have to be moving anywhere near the speed of light for this to happen.

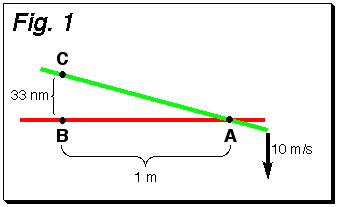
Consider the situation described in the figure below. One rod is fixed, the other is moving straight down at a (very easily obtainable) speed of 10 meters per second. The angle between the rods is very, very small, such that the distance from point C to point B is 33 nanometers (0.000000033 meters) and the distance between points A and B is one meter. At 10 meters per second, it will take 3.3 nanoseconds (0.0000000033 seconds) for point C to pass the fixed rod at point B. Since the distance between A and B is 1 meter, the "velocity" of the movement of the point of intersection is the distance traveled divided by the time of travel, which is 1 divided by 0.0000000033, or about 300000000 meters per second. This is the speed of light! If the moving rod was going faster than 10 meters per second, the intersection point would "move" faster than light. This does not violate any physical laws because there doesn't have to be any faster than light transfer of information for this to happen. If the rods were just passing each other, there would be no interaction whatsoever. In the cutting guillotine example, the same principle applies. Cutting is the breaking of a chemical bond. Referring to the diagram again, if a bond is broken at point A, and then another bond is broken at point B 3.3 nanoseconds later, the "cutting speed" would be the speed of light. No matter is actually moving faster than light. There are just a series of unconnected cutting events occurring in rapid succession. In fact, it would be physically impossible for point C to "know" about what point A was doing because that would involve FTL transfer of information. So even if the moving blade started to bend away from point A, that bending interaction could not propagate down to point C fast enough to influence its cutting at point B. As long as the angle BAC is shallow enough, FTL cutting is inevitable.

I hope this example helps without causing too much extra headache!

Megan- Can I help?!? Of course I can. I am, after all, what my wife calls an "answer slut." Luckily, she has an open mind with regard to helping my fellow humans with SCIENCE.

While I have been unable to accumulate the appropriate experimental results to fully support my answer, I'm pretty sure I know what's going on. In science terms, this is called an "educated guess."

At the molecular level, the wall of a popcorn kernel is composed of a hard form of starch, chains of sugar molecules chemically linked into a strong network (starch is nature's plastic). The network has very tiny pores in it. Since the popcorn kernel is nothing but a corn seed, it would require the pores to be just big enough to let water (a very small molecule - H₂O) and some inorganic nutrients inside. Salt is also very small, made up of just sodium and chlorine ions. These ions (single atoms with an electrical charge) can squeeze through pretty small spaces, so they get into the kernel without much problem.

Other flavorings, however, are made up of more complex organic molecules, much larger than salt. Although no flavoring I know of is as small as salt, there are a couple of small organic molecules that might make it through. I would suggest almond extract (benzaldehyde, just eight heavy atoms and 6 hydrogens), vanilla extract (vanillin, a bit bigger than benzaldehyde), and honey (glucose, a small carbohydrate - this has a good chance because the material that makes up the wall of the popcorn kernel is just a polymerized form of glucose). You would want to make these solutions very concentrated to increase the chances of membrane permeation (big words that mean "getting through the kernel wall").

More research will clearly be needed to back up my claims. Perhaps your step-sister would be willing to collaborate?

Chris- I might have to create a whole "Please Pass the Science: Relativistic Rods" section if this keeps up!

Your latest thought experiment is a good one, and you are correct that the point of intersection can be made to move very fast - even faster than light! In fact, if the two rods are precisely parallel, then each point will intersect at exactly the same moment. The intersection point would therefore be "moving" at infinite speed. I put moving in quotes because there is nothing actually moving faster than light, just the geometric point where the rods intersect. No information is transferred faster than light, and no weird physics is needed to explain the phenomenon.

Consider another example of a rod one light-minute long with thousands of tiny christmas lights strung along it. Each light is connected to a synchronized clock which can be programmed to flash the light at a precise time. I could then program the timers such that the flashes of light would appear to be "moving" extremely quickly down the length of the rod. The total time from the first light flash to the last light flash could be much less than one minute. Note that the point here is that these are individual events happening. No information is transferred from event to event, so the fact that the lighting of the bulbs "traverses" the rods faster than the speed of light is, quite frankly, no big deal. Events happen very closely together, even simultaneously, all the time in the real world.

Problems only arise when you try to accelerate something past the speed of light. When that happens, a "cause and effect" paradox may occur. That is, one could potentially witness the outcome of an event before its inception. In fact, Einstein's Special Theory of Relativity, the one that pretty much set this "speed limit" in the first place, is based around explaining why these paradoxes can happen if you exceed light speed. Since nobody has ever observed an effect happening before a cause (indeed, it would be pretty hard to even fathom such a situation), the speed limit is proven. This is a widely accepted way to prove something - to show how a logical inconsistency results from the negative of the proof. There is a very nice discussion of the Special Theory of Relativity at http://members.tripod.com/conduit9SR/. I strongly recommend it for anyone interested in travelling faster than light. It even directly addresses your question! (see "the classic giant guillotine" example on the final page)

Thanks, Matt, for the first Please Pass the Science follow-up answer!

Chris- You've come to the right place. Here at Please Pass the Science, we specialize in stuff that nobody else cares about!

As hard as it may be to believe, you are pretty much right on the mark, with regard to your question and presumed answers. The other end of the rod would indeed take a measurable amount of time to move, and it would almost certainly be less than the speed of light. I can understand why this may seem counter-intuitive. After all, a solid is, by definition, not very compressible. What you need to understand about this problem is that even at the atomic level, atoms take time to interact with each other. So what makes solids seem "solid", anyway? Well, it's simple electrostatic repulsion. When you push a rod, the negatively charged electrons in the atoms of your fingers repel the negatively charged electrons in the atoms of the rod. The resulting force pushes back on your finger. The nature of the electrostatic force has been worked out by physicists for some time now, and is understood to arise by the exchange of "virtual photons" between the two bodies interacting with each other. These virtual photons act just like normal photons (which are the individual particles which make up all electromagnetic radiation, including x-rays, radio waves and visible light), so they travel at the speed of light. Thus, any manifestation of electrostatic repulsion must occur within the boundaries of the speed of light.

In your thought experiment where you propose pushing a light-year long rod, it would indeed take at least a year for the atoms at one end of the rod to transmit the force of your initial push along its length. Think of a bunch of dominoes lined up in a long row. When you push the first one down, it knocks over the next one, then that one knocks over the next one, and so on until the last domino falls. The length of time that it takes for the all the dominoes to fall is dependent on the time it takes each individual domino to fall and knock over its neighbor. This is exactly what happens to the atoms in the rod. The electrostatic repulsion between electrons in each atom of the rod takes time to propagate through the whole rod, because it arises from the exchange of particles which cannot exceed the speed of light.

Similarly, if you pull the rod, you are pulling a set of atoms that are chemically bonded to the other rod atoms. Chemical bonds are also a manifestation of electrostatic interactions, and must obey the same rules as above. It takes a certain amount of time to transmit the pulling force through each atom of the rod, and thus, it would take time for this force to be transmitted through the length of the rod.

With regard to a rod made of neutron star material (or "neutronium", as high energy physicists like to call it), I'm afraid you still can't escape the speed of light limit. The forces which hold the nucleus together are called simply the strong and weak nuclear force. The carriers of these forces are gluons and the Z and W bosons. While it is true that the nucleus is extremely dense, it is still made up of particles which must interact through force carriers, which in turn cannot travel faster than light. I've talked with a couple of physicists about this, and the general consensus seems to be that if you were indeed able to construct a rod of neutronium and push it fast enough, it might compress enough to turn into a black hole, but it certainly would not move faster than the speed of light.

This whole pushing and pulling business could be addressed experimentally by synchronizing two highly accurate clocks (atomic clocks can measure very short intervals, on the order of 0.0000000000000001 seconds), placing them at opposite ends of a rod, and setting up a sensor such that each clock stops when its end of the rod moves. Pushing on one end of the rod should stop the clock on that end first, then the clock on the other side. There should be a difference in the time recorded on each clock, corresponding to the time it took for the force to propagate through the rod. My guess is that different materials would have different propagation times. Perhaps this experiment has already been done. Readers?

[ home | contact dr. berk | archive ]